Esercitazione 3

Soluzioni passo-passo esercizi per casa

Esercizio 1.2: istruzioni stringa, soluzione passo-passo

Ricordiamo la traccia dell'esercizio:

1. Leggere messaggio da terminale.
2. Convertire le lettere minuscole in maiuscolo, usando le istruzioni stringa.
3. Stampare messaggio modificato.

Le istruzioni stringa sono un esempio di set di istruzioni specializzate, cioè istruzioni che non sono pensate per implementare algoritmi generici, ma sono invece pensate per fornire supporto hardware efficiente a uno specifico set di operazioni che alcuni algoritmi necessitano. Infatti, ci si può aspettare che tra due programmi equivalenti, uno scritto con sole istruzioni generali e l'altro scritto con istruzioni specializzate, il secondo sarà molto più performante del primo. Altri esempi comuni sono le istruzioni a supporto di crittografia, encoding e decoding di stream multimediali, e, più recentemente, neural networks.

Questi set di istruzioni sono però più "rigidi" delle istruzioni a uso generale. Ci impongono infatti dei modi specifici di organizzare dati e codice, perché questi devono essere compatibili con il modo in cui l'algoritmo eseguito da un'istruzione è implementato in hardware.

Nell'esercizio 1.1 abbiamo considerato due modi di scorrere i due array. Nel primo, che è quello che abbiamo scelto, si carica l'indirizzo di inizio del vettore, e si usa un altro registro come indice, usando l'indirizzazione con indice. Nel secondo, si usa un registro come puntatore alla cella corrente, inizializzato all'indirizzo di inizio del vettore e poi incrementato (della quantità giusta) per passare all'elemento successivo. In entrambi i casi, siamo liberi di usare i registri che vogliamo, per esempio non abbiamo nessun problema se scriviamo il programma di prima come segue:

    lea msg_in, %eax
    lea msg_out, %ebx
    mov $0, %edx
loop:   
    movb (%eax, %edx), %cl
    ...

Infatti, usare esi ed edi come registri puntatori, ed ecx come registro di indice, è del tutto opzionale.

Tutto questo cambia quando si vogliono usare istruzioni specializzate come le istruzioni stringa. Queste ci impongono di usare esi come puntatore al vettore sorgente, edi come puntatore al vettore destinatario, eax come registro dove scrivere o da cui leggere il valore da trasferire, ecx come contatore delle ripetizioni da eseguire, etc. Una volta scelte le istruzioni da usare, dobbiamo quindi assicurarci di seguire quanto imposto dall'istruzione.

Per questo esercizio siamo interessati alla lods, che legge un valore dal vettore e ne sposta il puntatore allo step successivo, e la stos, che scrive un valore nel vettore. Partiamo dal riscrivere il punto_2 dell'esercizio 1.1 in modo da rendere l'algoritmo compatibile.

...
punto_2:
    lea msg_in, %esi
    lea msg_out, %edi
loop:
    movb (%esi), %al
    inc %esi
    cmp $'a', %al
    jb post_check
    cmp $'z', %al
    ja post_check
    and $0xdf, %al
post_check:
    movb %al, (%edi)
    inc %edi
    cmp $0x0d, %al
    jne loop
...

Abbiamo dunque rimosso l'uso di ecx come indice, e usiamo esi ed edi come puntatori. Il fatto di usare la inc è legato alla dimensione dei dati, cioè 1 byte. Dovremmo invece scrivere add $2, %esi o add $4, %esi per dati su 2 o 4 byte. Altra nota è che incrementiamo i puntatori, anziché decrementarli, perché stiamo eseguendo l'operazione da sinistra verso destra.

Siamo pronti adesso a sostituire le istruzioni evidenziate con delle istruzioni stringa. Il sorgente finale è scaricabile qui.

...
punto_2:
    lea msg_in, %esi
    lea msg_out, %edi
    cld
loop:
    lodsb
    cmp $'a', %al
    jb post_check
    cmp $'z', %al
    ja post_check
    and $0xdf, %al
post_check:
    stosb
    cmp $0x0d, %al
    jne loop
...

L'istruzione cld serve a impostare a 0 il flag di direzione, che serve a indicare alle istruzioni stringa se andare da sinistra verso destra o il contrario. Dato che tutti i registri sono impliciti, dobbiamo sempre specificare la dimensione delle istruzioni, in questo caso b.

Come esercizio, può essere interessante osservare con il debugger l'evoluzione dei registri, osservando come si eseguono più operazioni con una sola istruzione.

Esercizio 1.6: esercizio di debugging, soluzione passo-passo

Ricordiamo la traccia dell'esercizio:

Scrivere un programma che, a partire dalla sezione .data che segue (e scaricabile qui), conta e stampa il numero di occorrenze di numero in array.

.include "./files/utility.s"

.data
array:      .word 1, 256, 256, 512, 42, 2048, 1024, 1, 0
array_len:  .long 9
numero:     .word 1

Questa è invece la soluzione proposta dall'esercizio:

.include "./files/utility.s"

.data
array:      .word 1, 256, 256, 512, 42, 2048, 1024, 1, 0
array_len:  .long 9
numero:     .word 1

.text

_main:
    nop
    mov $0, %cl
    mov numero, %ax
    mov $0, %esi

comp: 
    cmp array_len, %esi
    je fine
    cmpw array(%esi), %ax
    jne poi
    inc %cl

poi:  
    inc %esi
    jmp comp

fine: 
    mov %cl, %al
    call outdecimal_byte
    ret

Come prima cosa, cerchiamo di capire, a grandi linee, cosa cerca di fare questo programma.

Notiamo l'uso di %cl: dall'inizializzazione a riga 12, l'incremento condizionato a righe 19-21, e la stampa a righe 28-29, si evince che %cl è usato come contatore dei successi, ossia di quante volte è stato trovato numero in array. Notiamo che %ax viene inizializzato con numero e, prima della stampa, mai aggiornato. Infine, %esi viene inizializzato a 0 e incrementato a fine di ogni ciclo, confrontandolo con array_len per determinare quando uscire dal loop. Infine, a riga 19 notiamo il confronto tra un valore di array, indicizzato con %esi, e %ax, che contiene numero.

Si ricostruisce quindi questa logica: scorro valore per valore array, indicizzandolo con %esi, e lo confronto con numero, che è appoggiato su %ax (perché il confronto tra due valori in memoria non è possibile con cmp). Utilizzo %cl come contatore dei successi, e alla fine dello scorrimento ne stampo il valore.

Fin qui nessuna sorpresa, il programma sembra seguire lo schema che si seguirebbe con un normale programma in C:

int cl = 0;
for(int esi = 0; esi < array_len; esi++){
    if(array[esi] == numero)
        cl++;
}

Proviamo ad eseguire il programma: ci si aspetta che stampi 2. Invece, stampa 3. Dobbiamo passare al debugger.

Quello che ci conviene guardare è quello che succede ad ogni loop, in particolare alla riga 19, dove la cmpw confronta un valore di array con %ax, che contiene numero. Però, la cmpw utilizza un indirizzamento complesso che, come descritto nella documentazione, richiede una sintassi più complicata nel debugger. Cambio quindi quella istruzione in una serie equivalente che sia più facile da osservare col debugger.

.include "./files/utility.s"

.data
array:      .word 1, 256, 256, 512, 42, 2048, 1024, 1, 0
array_len:  .long 9
numero:     .word 1

.text

_main:
    nop
    mov $0, %cl
    mov numero, %ax
    mov $0, %esi

comp: 
    cmp array_len, %esi
    je fine
    movw array(%esi), %bx
    cmpw %bx, %ax
    jne poi
    inc %cl

poi:  
    inc %esi
    jmp comp

fine: 
    mov %cl, %al
    call outdecimal_byte
    ret

Assemblo, avvio il debugger, e setto un breakpoint alla riga 20 con break 20. Lascio girare il programma con continue, che quasi immediatamente raggiunge la riga 20 e si ferma. Ricordiamo che il debugger si ferma prima di eseguire una istruzione.

Vediamo lo stato dei registri, con i r ax bx cl esi (mostra solo quelli che ci interessano).

(gdb) i r ax bx cl esi
ax             0x1                 1
bx             0x1                 1
cl             0x0                 0
esi            0x0                 0

Fin qui, tutto come ci si aspetta: %ax che contiene numero, %bx contiene il numero alla prima cella di array, i due contatori %cl e %esi sono a 0. Facciamo step per vedere l'esito del confronto: dopo la riga 21 l'esecuzione giunge alla riga 22, indicando che il salto non è stato fatto perché la jne è stata eseguita dopo un confronto tra valori uguali.

Continuiamo con step controllando che il comportamento sia quello atteso, fino a giungere di nuovo alla riga 20.

(gdb) i r ax bx cl esi
ax             0x1                 1
bx             0x0                 0
cl             0x1                 1
esi            0x1                 1

Qui abbiamo la prima sorpresa. In %bx troviamo 0, ma il secondo valore di array è 256. Se continuiamo, vediamo che 256 compare come terzo valore, poi 1 come quarto, poi 256 come quinto. Abbiamo quindi dei valori aggiuntivi che compaiono durante lo scorrimento del vettore ma che non sono presenti nell'allocazione a riga 4. Continuando ancora, vediamo che i 9 valori coperti dal programma non sono affatto tutti e 9 quelli a riga 4, e che effettivamente il valore 1 compare 3 volte.

Con questo, abbiamo intanto confinato il problema: la logica di confronto e conteggio funziona, il problema è nella lettura di valori da array.

Per capire cosa sta succedendo, dobbiamo ricordare come si comporta l'allocazione in memoria di valori su più byte: abbiamo infatti a che fare con word, composte da 2 byte ciascuna, e ciascun indirizzo in memoria corrisponde a una locazione di un solo byte.

L'architettura x86 è little-endian, che significa little end first, un riferimento a I viaggi di Gulliver. Questo si traduce nel fatto che quando un valore di $n$ byte viene salvato in memoria a partire dall'indirizzo $a$, il byte meno significativo del valore viene salvato in $a$, il secondo meno significativo in $a+1$, e così via fino al più significativo in $a+(n-1)$.

Possiamo quindi immaginare così il nostro array in memoria.

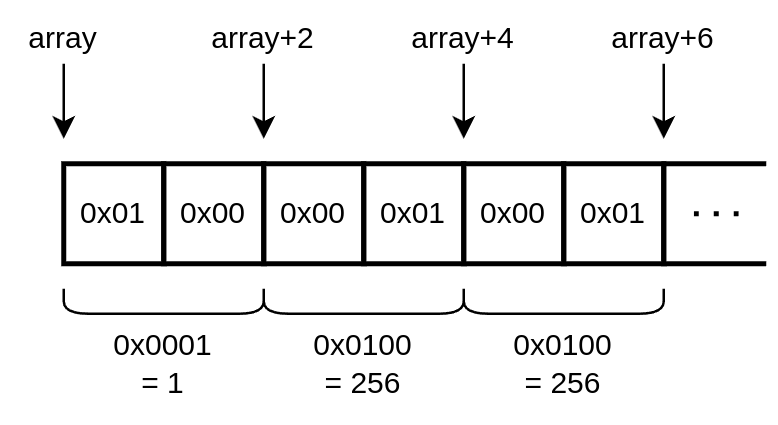
Layout di array in memoria.

La lettura di una word dalla memoria funziona quindi così: dato l'indirizzo $a$, vengono letti i due byte agli indirizzi $a$ e $a+1$ e contatenati nell'ordine $(a+1, a)$. Una istruzione come movw a, %bx, quindi, salverà il contenuto di $a+1$ in %bh e il contenuto di $a$ in %bl.

Per la lettura di più word consecutive, dobbiamo assicurarci di incrementare l'indirizzo di 2 alla volta: come mostrato in figura, il secondo valore è memorizzato a partire da $array+2$, il terzo da $array+4$, e così via.

Tornando però al codice dell'esercizio, questo non succede:

comp: 
    cmp array_len, %esi
    je fine
    movw array(%esi), %bx
    cmpw %bx, %ax
    jne poi
    inc %cl

poi:  
    inc %esi
    jmp comp

Ecco quindi spiegato cosa legge il programma dalla memoria: quando alla seconda iterazione si esegue movb array(%esi), %bx, con %esi che vale 1, si sta leggendo un valore composto dal byte meno significativo del secondo valore concatenato con il byte più significativo del primo. Questo valore è del tutto estraneo e privo di senso se confrontato con array così come è stato dichiarato e allocato, ma nell'eseguire le istruzioni il processore non sa e non controlla niente di tutto ciò.

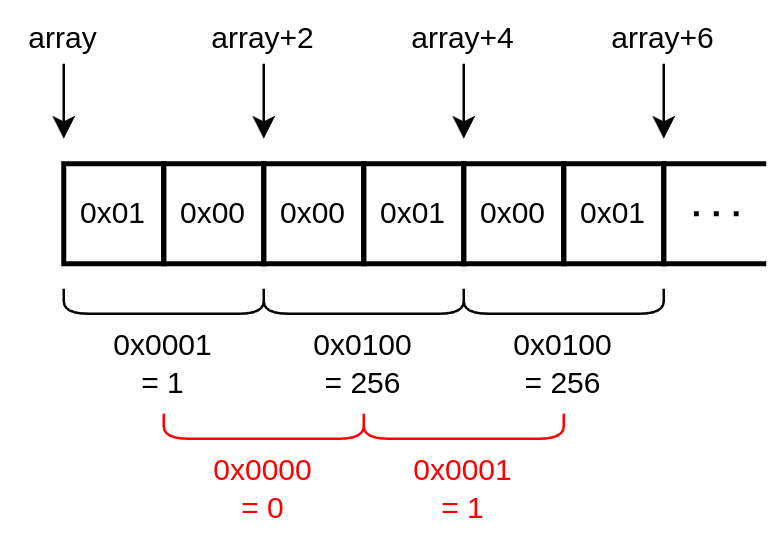
Lettura erronea di array: sbagliando l'incremento dell'indirizzo, leggiamo dei byte senza alcuna relazione fra loro dalla memoria e li interpretiamo come parti di una word.

Abbiamo due strade per correggere questo errore. Il primo approccio è quello di incrementare %esi di 2 alla volta, così che l'indirizzamento array(%esi) risulti corretto. Con questo schema però %esi dovrà assumere i valori $0, 2, \dots 16$, cosa che lo rende non più un contatore confrontabile direttamente con array_len come fatto a riga 17. Si dovrà gestire tale confronto in altro modo, per esempio usando un registro separato come contatore.

La seconda strada è quella di usare il fattore di scala dell'indirizzamento, che è pensato proprio per essere utilizzato in casi come questo. Infatti, array(, %esi, 2) calcolerà l'indirizzo $array + 2 * esi$. Da notare la virgola subito dopo la parentesi, che sta a indicare che il registro base è stato omesso, mentre %esi è indice.

Per concludere, torniamo sul codice C che abbiamo visto prima come modello di questo programma: come viene gestito lì questo problema? In quel codice C non vi è alcun errore perché array[esi], sfruttando la tipizzazione e l'aritmetica dei puntatori, applica sempre i fattori di scala corretti. Infatti, mentre il processore che esegue istruzioni assembler non ha idea del significato di tali istruzioni, linguaggi di livello più alto introducono concetti come i tipi proprio per permettere di esprimere questi significati e occuparsene a tempo di compilazione per produrre assembler corretto.

Il codice finale, scaricabile qui, è il seguente:

.include "./files/utility.s"

.data
array:      .word 1, 256, 256, 512, 42, 2048, 1024, 1, 0
array_len:  .long 9
numero:     .word 1

.text

_main:
    nop
    mov $0, %cl
    mov numero, %ax
    mov $0, %esi

comp: 
    cmp array_len, %esi
    je fine
    cmpw array(, %esi, 2), %ax
    jne poi
    inc %cl

poi:  
    inc %esi
    jmp comp

fine: 
    mov %cl, %al
    call outdecimal_byte
    ret

Esercizio 3.1: esercizio d'esame 2021-01-08

Il testo con soluzione si trova qui.

Provare da sé

Provare a svolgere da sé l'esercizio, prima di guardare la soluzione o andare oltre per la discussione.

Questo esercizio pone principalmente tre spunti.

Il primo è la gestione dell'input, da eseguire con un loop di inchar e controlli, facendo outchar solo quando il carattere è accettato. Questo è stato già visto, per esempio, nell'esercizio 2.1.

Il secondo spunto riguarda il dimensionamento dei dati da gestire. Infatti, dobbiamo scegliere se usare 8, 16 o 32 bit, e possiamo farlo solo cercando di capire su quanti bit sta il numero più grande che possiamo gestire.

Data la natura del problema, è facile intuire che questo si trova quando $N = 9$ e $k = 9$. Dovremmo stampare un triangolo 9 righe, ciascuna composta da 1 a 9 numeri, a partire da 1 e di passo 9. Da una parte, potremmo ricordarci questa è una sequenza nota: la somma di $1 + 2 + ... + n$ è $\frac{n(n+1)}{2}$, quindi abbiamo $9 \cdot 10/2 = 45$ elementi. Tuttavia, un approccio più semplice porta a un risultato simile: di sicuro il triangolo avrà meno elementi di un quadrato di lato 9, composto da $9 \cdot 9 = 81$ elementi e, dato che la diagonale è inclusa, avrà più della metà di questo, cioè $81 / 2$. Possiamo quindi dire con questo ragionamento che sono più di $41$ elementi e meno di $81$, mentre usando la formula esatta troviamo che sono $45$.

Dato che incrementiamo di passo 9 ogni volta, il numero di posizione $j$ sarà $(j-1) \cdot 9 + 1$. Considerando per la stima di prima il 41-esimo elemento, abbiamo $40 \cdot 9 + 1 = 361$, mentre l'81-esimo elemento (che non sarà mai presente) sarebbe $80 \cdot 9 + 1 = 721$. Il valore esatto, se ci ricordiamo la formula di cui sopra, è invece $44 \cdot 9 + 1 = 397$. Un tale numero deve essere rappresentato su più di 8 bit, ma sta senza problemi in 16 bit: svolgeremo quindi i nostri calcoli usando delle word di 16 bit.

Non resta quindi che fare la stampa del triangolo. Questo si può scrivere come un doppio loop, dove il loop interno usa il contatore esterno per determinare quando uscire stampando una nuova riga, mentre un registro contatore viene utilizzato durante ogni ciclo per calcolare il nuovo numero da stampare. In (pseudo) C, tale ciclo avrebbe una forma simile:

short c = 1; // word da 16 bit
for(int i = 0; i < n; i++) {
    for(int j = 0; j < i + 1; j++) {
        outdecimal_word(c);
        outchar(' ');
        c += k;
    }
    outline()
}

Esercizi per casa

Esercizio 3.2

Scrivere un programma che svolge quanto segue.

# leggere 2 numeri interi in base 10, calcolarne il prodotto, e stampare il risultato.

# lettura:
# come primo carattere leggere il segno del numero, cioè un '+' o un '-'
# segue il modulo del numero, minore di 256

# stampa:
# stampare prima il segno del numero (+ o -), poi il modulo in cifre decimali

Esercizio 3.3

Quello che segue (e scaricabile qui) è un tentativo di soluzione dell'esercizio precedente. Contiene tuttavia uno o più bug. Trovarli e correggerli.

.include "./files/utility.s"

mess1:  .asciz "inserire il primo numero intero:\r" 
mess2:  .asciz "inserire il secondo numero intero:\r"
mess3:  .asciz "il prodotto dei due numeri e':\r"
a:      .word 0
b:      .word 0

_main:      
    nop
    lea mess1, %ebx
    call outline
    call in_intero
    mov %ax, a

    lea mess2, %ebx
    call outline
    call in_intero
    mov %ax, b

    mov a, %ax
    mov b, %bx
    imul %bx

    lea mess3, %ebx
    call outline
    call out_intero
    ret

# legge un intero composto da segno e modulo minore di 256
# ne lascia la rappresentazione in complemento alla radice base 2 in ax
in_intero:
    push %ebx
    mov $0, %bl
in_segno_loop:   
    call inchar
    cmp $'+', %al
    je in_segno_poi
    cmp $'-', %al
    jne in_segno_loop
    mov $1, %bl
in_segno_poi:
    call outchar
    call indecimal_word
    call newline
    cmp $1, %bl
    jne in_intero_fine
    neg %ax
in_intero_fine:
    pop %ebx
    ret

# legge la rappresentazione di un numero intero in complemento alla radice base 2 in eax
# lo stampa come segno seguito dalle cifre decimali
out_intero:
    push %ebx
    mov %eax, %ebx
    cmp $0, %ebx
    ja out_intero_pos
    jmp out_intero_neg
out_intero_pos:
    mov $'+', %al
    call outchar
    jmp out_intero_poi
out_intero_neg:
    mov $'-', %al
    call outchar
    neg %ebx
    jmp out_intero_poi
out_intero_poi:
    mov %ebx, %eax
    call outdecimal_long
    pop %ebx
    ret

Soluzione passo-passo

Per brevità, e vista la documentazione dei sottoprogrammi, lascio al lettore l'interpretazione a grandi linee del programma. Passeremo direttamente ai problemi incontrati testando il programma.

inserire il primo numero intero:
+30
Segmentation fault

L'errore, sicuramente già ben noto, è in realtà un risultato tipico di una vasta gamma di errori. Di per sé significa semplicemente "tentativo di accesso in una zona di memoria a cui non si può accedere per fare quello che si voleva fare". Non spiega, per esempio, cos'è che si voleva fare e perché è sbagliato.

Vediamo tramite il debugger.

Program received signal SIGSEGV, Segmentation fault.
    _main () at /mnt/c/reti_logiche/assembler/lezioni/2/imul_debug.s:14
14          mov %ax, a

Questo ci dice che il problema è il tentativo di scrivere all'indirizzo $a$, che è la word allocata poco più su. Il problema qui è che il programma non ha nessuna distinzione tra .data e .text: di default è tutto .text, dove non si può scrivere perché non ci è permesso, normalmente, sovrascrivere le istruzioni del programma. Il problema inverso si avrebbe tentando di eseguire dalla sezione .data.

Correggiamo l'errore aggiungendo le dichiarazioni di queste due sezioni.

.include "./files/utility.s"

.data
mess1:  .asciz "inserire il primo numero intero:\r" 
mess2:  .asciz "inserire il secondo numero intero:\r"
mess3:  .asciz "il prodotto dei due numeri e':\r"
a:      .word 0
b:      .word 0

.text
_main:
...

Ritestiamo quindi il programma:

inserire il primo numero intero:
+30
inserire il secondo numero intero:
+20
il prodotto dei due numeri e':
+600

Fin qui, sembra andare bene. Ricordiamoci però di testare tutti i casi di interesse, in particolare i casi limite. Le specifiche dell'esercizio ci chiedono di considerare numeri interi di modulo inferiore a 256.

inserire il primo numero intero:
+255
inserire il secondo numero intero:
+255
il prodotto dei due numeri e':
+65025

Corretto.

inserire il primo numero intero:
-255
inserire il secondo numero intero:
+255
il prodotto dei due numeri e':
+511

Decisamente non corretto. Verifichiamo col debugger. Per prima cosa, ci assicuriamo che la lettura di numeri negativi sia corretta. Mettiamo un brekpoint a riga 16 (riga 14 prima dell'aggiunta di .data e .text), e verifichiamo cosa viene letto quando inseriamo -255.

(gdb) b 16
Breakpoint 2 at 0x56556774: file /mnt/c/reti_logiche/assembler/lezioni/2/imul_debug.s, line 16.
(gdb) c
Continuing.
inserire il primo numero intero:
-255

Breakpoint 2, _main () at /mnt/c/reti_logiche/assembler/lezioni/2/imul_debug.s:16
16          mov %ax, a
(gdb) i r ax
ax             0xff01              -255
(gdb)

Fin qui è bene, il problema non sembra essere nella lettura di interi da tastiera. Proseguiamo quindi alla moltiplicazione, e controlliamone il risultato. La imul utilizzata è a 16 bit, che da documentazione vediamo usa %ax come operando implicito, %bx come operando esplicito, e %dx_%ax come destinatario del calcolo.

Breakpoint 3, _main () at /mnt/c/reti_logiche/assembler/lezioni/2/imul_debug.s:25
25          imul %bx
(gdb) i r ax bx
ax             0xff01              -255
bx             0xff                255
(gdb) s
27          lea mess3, %ebx
(gdb) i r dx ax
dx             0xffff              -1
ax             0x1ff               511
(gdb)

Concatenando i due registri otteniamo 0xffff01ff, ricordando, in particolare per %ax, che gdb omette nelle stampe gli zeri all'inizio di esadecimali. Possiamo verificare questo valore convertendo da esadecimale a decimale con una calcolatrice da programmatore. Dato che si parla di interi, è importante impostare la calcolatrice sul numero di bit giusti, in questo caso 32. Nella calcolatrice di Windows, questo significa impostare la modalità DWORD.

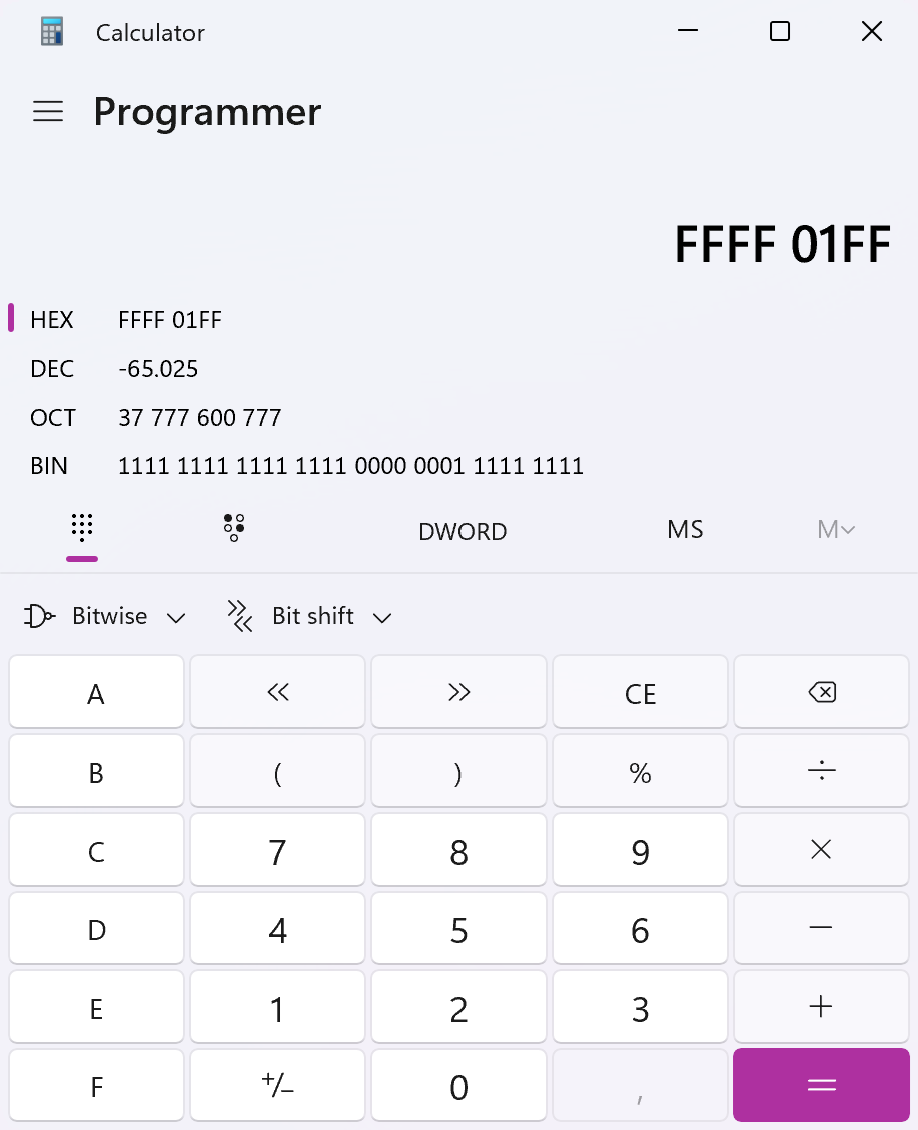
Uso della calcolatrice da programmatore in Windows 11 per convertire da esadecimale a intero decimale.

Il risultato è -65025, che è quello che ci aspettiamo. Anche qui, quindi, è bene: resta allora la stampa di questo valore, cioè il sottoprogramma out_intero.

# legge la rappresentazione di un numero intero in complemento alla radice base 2 in eax
# lo stampa come segno seguito dalle cifre decimali
out_intero:
    ...

Vediamo qui la prima discrepanza: il sottoprogramma si aspetta il risultato in %eax, ma noi sappiamo che la imul lo lascia in %dx_%ax. Ci si può chiedere quale dei due correggere, se il sottoprogramma o il programma che lo usa. In generale, è una buona cambiare le specifiche di un componente interno (il sottoprogramma) solo quando queste non hanno senso. È quindi il componente esterno (il programma) che non rispetta le specifiche d'uso di quello interno, e che va cambiato.

Assicuriamoci allora di lasciare il risultato nel registro giusto prima di call out_intero.

...
    mov a, %ax
    mov b, %bx
    imul %bx

    shl $16, %edx
    movw %ax, %dx
    movl %edx, %eax

    lea mess3, %ebx
    call outline
    call out_intero
...

Riproviamo ad eseguire:

inserire il primo numero intero:
-255
inserire il secondo numero intero:
+255
il prodotto dei due numeri e':
+4294902271

Il risultato è cambiato, ma è comunque sbagliato. Ritorniamo al debugger, cominciando dalla call di out_intero, verificando di avere il valore corretto in %eax.

Breakpoint 2, _main () at /mnt/c/reti_logiche/assembler/lezioni/2/imul_debug.s:33
33          call out_intero
(gdb) i r eax
eax            0xffff01ff          -65025
(gdb) 

Il valore in %eax è corretto, il problema allora è nel sottoprogramma. Proseguiamo nel sottoprogramma, cercando di capire come funziona e dove potrebbe sbagliare. La prima cosa che notiamo è che out_intero ha due rami, out_intero_pos e out_intero_neg, dove stampa segni diversi e, in caso di numero negativo, usa la neg per ottenere l'opposto. Quando si giunge a out_intero_poi, stampa il modulo del numero usando outdecimal_long (che, ricordiamo, supporta solo numeri naturali). Tuttavia, nella nostra esecuzione abbiamo un negativo che viene stampato come naturale.

Verifichiamo seguendo l'esecuzione con step, che entra nel sottoprogramma out_intero:

(gdb) s
out_intero () at /mnt/c/reti_logiche/assembler/lezioni/2/imul_debug.s:62
62          push %ebx
(gdb) s
63          mov %eax, %ebx
(gdb) s
64          cmp $0, %ebx
(gdb) i r ebx
ebx            0xffff01ff          -65025
(gdb) s
65          ja out_intero_pos
(gdb) s
out_intero_pos () at /mnt/c/reti_logiche/assembler/lezioni/2/imul_debug.s:68
68          mov $'+', %al
(gdb) 

Effettivamente, nonostante %ebx sia un numero negativo, il salto a out_intero_pos viene eseguito. Guardiamo però più attentamente: l'istruzione di salto è ja, che interpreta il confronto come tra numeri naturali. In effetti, qualunque valore di %ebx diverso da 0, se interpretato come naturale, risulta maggiore di 0. Correggiamo quindi utilizzando jg, e ritestiamo.

    cmp $0, %ebx
    jg out_intero_pos
    jmp out_intero_neg

inserire il primo numero intero:
-255
inserire il secondo numero intero:
+255
il prodotto dei due numeri e':
-65025

Si dovrebbe ora continuare con altri test (combinazioni di segni, uso di 0) fino a convincersi che funzioni. Per questa soluzione ci fermiamo qui.

Il codice finale, scaricabile qui, è il seguente:

.include "./files/utility.s"

.data
mess1:  .asciz "inserire il primo numero intero:\r" 
mess2:  .asciz "inserire il secondo numero intero:\r"
mess3:  .asciz "il prodotto dei due numeri e':\r"
a:      .word 0
b:      .word 0

.text
_main:      
    nop
    lea mess1, %ebx
    call outline
    call in_intero
    mov %ax, a

    lea mess2, %ebx
    call outline
    call in_intero
    mov %ax, b

    mov a, %ax
    mov b, %bx
    imul %bx

    shl $16, %edx
    movw %ax, %dx
    movl %edx, %eax

    lea mess3, %ebx
    call outline
    call out_intero
    ret

# legge un intero composto da segno e modulo minore di 256
# ne lascia la rappresentazione in complemento alla radice base 2 in ax
in_intero:
    push %ebx
    mov $0, %bl
in_segno_loop:   
    call inchar
    cmp $'+', %al
    je in_segno_poi
    cmp $'-', %al
    jne in_segno_loop
    mov $1, %bl
in_segno_poi:
    call outchar
    call indecimal_word
    call newline
    cmp $1, %bl
    jne in_intero_fine
    neg %ax
in_intero_fine:
    pop %ebx
    ret

# legge la rappresentazione di un numero intero in complemento alla radice base 2 in eax
# lo stampa come segno seguito dalle cifre decimali
out_intero:
    push %ebx
    mov %eax, %ebx
    cmp $0, %ebx
    jg out_intero_pos
    jmp out_intero_neg
out_intero_pos:
    mov $'+', %al
    call outchar
    jmp out_intero_poi
out_intero_neg:
    mov $'-', %al
    call outchar
    neg %ebx
    jmp out_intero_poi
out_intero_poi:
    mov %ebx, %eax
    call outdecimal_long
    pop %ebx
    ret

Esercizio 3.4

Quello che segue (e scaricabile qui) è un tentativo di soluzione per le seguenti specifiche:

# Leggere una riga dal terminale, che DEVE contenere almeno 2 caratteri '_'
# Identificare e stampa la sottostringa delimitata dai primi due caratteri '_'

Un esempio di output (qui in formato txt) è il seguente

questa e' una _prova_ !!
prova

Contiene tuttavia uno o più bug. Trovarli e correggerli.

.include "./files/utility.s"

.data

msg_in: .fill 80, 1, 0

.text
_main:  
    nop
    mov $80, %cx
    lea msg_in, %ebx
    call inline

    cld
    mov $'_', %al
    lea msg_in, %esi
    mov $80, %cx

    repne scasb
    mov %esi, %ebx
    repne scasb
    mov %esi, %ecx
    sub %ebx, %ecx
    call outline

    ret

Soluzione

Il programma usa repne scasb per scorrere il vettore finché non trova il carattere in %al, cioè _. Dopo la prima scansione, salva l'indirizzo attuale per usarlo come indirizzo di partenza della sottostringa. Dopo la seconda scansione, fa una sottrazione di indirizzi per trovare il numero di caratteri che compongono la sottostringa. Usando indirizzo di partenza e numero caratteri, stampa quindi a terminale.

I bug da trovare sono i seguenti:

• Le istruzioni rep utilizzano %ecx, ma la riga 17 inizializza solo %cx. Questo funziona solo se, per puro caso, la parte alta di %ecx è a 0 ad inizio programma.
• L'istruzione scasb ha l'indirizzo del vettore come destinatario implicito in %edi, non %esi.
• La repne scasb termina dopo aver scansionato il carattere che rispetta l'equivalenza. Questo vuol dire che dopo la prima scansione abbiamo l'indirizzo del carattere dopo il primo _ (corretto) ma dopo la seconda scansione abbiamo l'indirizzo del carattere dopo il secondo _: la sottrazione calcola una sottostringa che include il _ di terminazione.
• Il sottoprogramma usato è quello sbagliato: outline stampa finché non incrontra \r, per indicare il numero di caratteri da stampare va usato outmess.

Il codice dopo le correzioni è quindi il seguente, scaricabile qui.

.include "./files/utility.s"

.data

msg_in: .fill 80, 1, 0

.text
_main:  
    nop
    mov $80, %cx
    lea msg_in, %ebx
    call inline

    cld
    mov $'_', %al
    lea msg_in, %edi
    mov $80, %cx

    repne scasb
    mov %edi, %ebx
    repne scasb
    mov %edi, %ecx
    sub %ebx, %ecx
    dec %ecx
    call outmess

    ret

Si sottolinea inoltre una debolezza della soluzione: la sottrazione fra puntatori funziona solo perché la scala è 1, cioè maneggiamo valori da 1 byte, per cui c'è corrispondenza fra la differenza di due indirizzi e il numero di elementi fra loro. Una soluzione più robusta è utilizzare la differenza del contantore %ecx anziché di puntatori. In alternativa, si può utilizzare shift a destra dopo la sottrazione per tener conto di una scala maggiore di 1, ma è un metodo che rende facile sbagliare (bisogna stare attenti all'ordine tra shift e decremento).

Si può verificare ciò svolgendo un esercizio simile a questo basato ma basato su word, per esempio con serie di valori decimali delimitati da 0.

Esercizio 3.5

A partire dalla soluzione dell'esercizio precedente, estendere il programma per rispettare le seguenti specifiche:

# Leggere una riga dal terminale
# Identificare e stampa la sottostringa delimitata dai primi due caratteri '_'
# Se un solo carattere '_' e' presente, assumere che la sottostringa cominci 
# ad inizio stringa e finisca prima del carattere '_'
# Se nessun carattere '_' e' presente, stampare l'intera stringa

Soluzione

Il programma dell'esercizio 3.4 viene complicato dalla richiesta di gestire dei valori di default, in caso siano presenti uno o nessun delimitatore _. Questo vuol dire gestire il caso in cui una repne scasb termina non perché ha trovato il carattere, ma perché %ecx è stato decrementato fino a 0.

Questo si implementa come dei semplici check su %ecx dopo ciascuna repne scasb, in caso sia 0 si va a un branch separato: se succede alla prima scansione non è presente alcun _ e saltiamo quindi a print_all, se succede alla seconda scansione abbiamo solo un _ e saltiamo quindi a print_from_start. Altrimenti, si prosegue con lo stesso codice dell'esercizio 2.2, che nomineremo print_substr.

Per print_all basta una semplice outline dell'intera stringa. Per print_from_start, si fa un ragionamento non dissimile da quanto visto per l'esercizio precedente, dove va usato come inizio l'indirizzo di msg_in e il numero di caratteri può essere calcolato, come prima, usando l'indirizzo che troviamo in %edi dopo la prima repne scasb.

Il codice risultante è il seguente, scaricabile qui.

.include "./files/utility.s"

.data

msg_in: .fill 80, 1, 0

.text
_main:  
    nop
    mov $80, %cx
    lea msg_in, %ebx
    call inline

    cld
    mov $'_', %al
    lea msg_in, %edi
    mov $80, %ecx

    repne scasb
    cmp $0, %ecx
    je print_all

    mov %edi, %ebx
    repne scasb
    cmp $0, %ecx
    je print_from_start

print_substr:
    mov %edi, %ecx
    sub %ebx, %ecx
    dec %ecx
    call outmess
    ret

print_from_start:
    mov %ebx, %ecx
    lea msg_in, %ebx
    sub %ebx, %ecx
    dec %ecx
    call outmess
    ret

print_all:
    lea msg_in, %ebx
    call outline
    ret